The Lenz-Ising model (and cellular automata) simulators
The Lenz-Ising model (often more simply called ‘the Ising model’), developed by Ernst Ising and Wilhelm Lenz in 1925, is a simple mathematical model used to study magnetism in statistical physics. It consists of discrete variables called spins, which can be in one of two states (+1 or -1), arranged on a lattice where each spin interacts with its neighbours. Despite its simplicity, the Ising model has profound applications, extending beyond magnetism to areas such as neural networks, social dynamics, and computational biology. It serves as a foundational tool to explore complex systems and emergent behaviour.
In the Laboratory of Artificial& Natural Evolution, we use the Ising model on a hexagonal lattice to study the skin colour patterns in lizards which display scale-by-scale coloration. The variables (+1) and (-1) account for green and black colour scales, respectively. Although the classical Lenz-Ising model includes only two parameters — the external magnetic field (B, which can be loosely interpreted as self-interaction) and the first-neighbour interaction (J1) — we use its more general form that additionally includes a second-neighbour interaction term and a ‘plaquette’ term that favours or hinders three direct neighbours to have the same state.
Below, we present two implementations of the Ising model: a single-flip and a spin-exchange scheme, as well as the original (square) Game of Life and an hexagonal variation of it. All codes are implemented by James Headon under the supervision of ‘Meti’ Ibrahimi and Szabolcs Zakany.
The Simulator
Ising model:
Spin-like interactions:

Total energy (
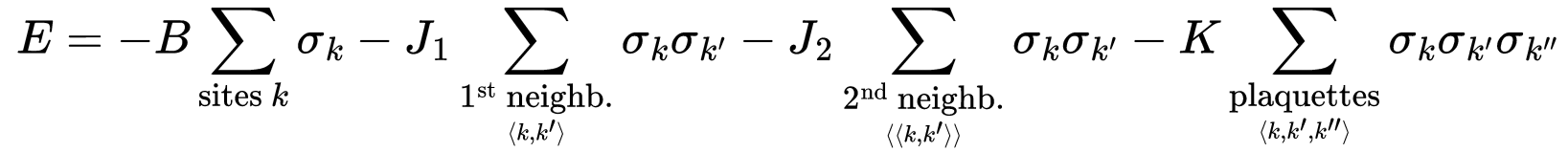
Conway's classic Game of Life:
The rules are "B2/S23" on a square lattice (each cell has 8 neighbours):
- A black cell becomes green if it has exactly 2 green nearest neighbours ("B2")
- A green cell stays green if it has 2 or 3 green neighbours ("S23")
- Otherwise, all cells become black
A hexagonal version of the Game of Life:
The rules are "H:B2/S34" on the hexagonal lattice ("H", each cell has 6 neighbours):
- A black cell becomes green if it has exactly 2 green neighbours("B2")
- A green cell stays green if it has 3 or 4 green neighbours ("S34")
- Otherwise, all cells become black.